1. Find the first derivative formula for each function. In each case tak with respect to the independent variable as implied by the expressi side of the equal sign. For full-credit, use the appropriate name for simplify your results completely, leaving no negative or rational exp not use the product or quotient rules in situations where the consta or the power rule is applicable. -1 1 (a) f(x) %3D VI 12 (b) h(x): 4 3. %3D 24
1. Find the first derivative formula for each function. In each case tak with respect to the independent variable as implied by the expressi side of the equal sign. For full-credit, use the appropriate name for simplify your results completely, leaving no negative or rational exp not use the product or quotient rules in situations where the consta or the power rule is applicable. -1 1 (a) f(x) %3D VI 12 (b) h(x): 4 3. %3D 24
Which rule do I use? The answer for the first one is (-1/x^2)-1/2((squareroot)x^3). I just don't know how to get that answer.
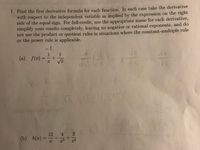
Transcribed Image Text:### Calculus: Finding the First Derivative
#### Problem Statement:
1. **Objective:** Find the first derivative formula for each function. Take the derivative with respect to the independent variable as indicated by the expression on the right side of the equal sign. To achieve full credit, adhere to the following:
- Use the appropriate name for each derivative.
- Simplify your results completely.
- Avoid negative or rational exponents.
- Refrain from using the product or quotient rules when the constant-multiple rule or the power rule is applicable.
#### Functions to Differentiate:
(a) \( f(x) = \frac{1}{x} + \frac{1}{\sqrt{x}} \)
(b) \( h(x) = \frac{12}{x} - \frac{4}{x^3} + \frac{3}{x^4} \)
**Instructions for Solution:**
- Identify the applicable rules for differentiation.
- Simplify expressions to ensure the absence of negative or rational exponents.
- Ensure the use of the simplest methods before complex rules when applicable.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning