Question
thumb_up100%
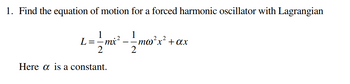
Transcribed Image Text:1. Find the equation of motion for a forced harmonic oscillator with Lagrangian
= mx ² - 1/mo ² x ²
L=-mx
Here a is a constant.
+ ax
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 3 images

Knowledge Booster
Similar questions
- 9. Solve the coupled oscillator system such that m₁ = m² = 1, k₁ = k3 = 9,k₂ = 8. Assume the first mass is pushed 2 units to the right of equilibrium and the 2nd 2 units to the left of equilibrium, with zero initial velocities. Describe the behavior of the motions of the masses at each of the nodes.arrow_forwardFind the equation of simple harmonic motion for a spring mass system where the mass is hanging off the ceiling with the help of a spring if the initial displacement is 1 ft above equilibrium with initial upward velocity of 2 ft/s. Assume w=1. Write in form y=Asin(x+b). Solve for A, x, and b.arrow_forwardA mass of 0.38 kg is attached to a spring and set into oscillation on a horizontal frictionless surface. The simple harmonic motion of the mass is described by x(t) = (0.26 m)cos[(16 rad/s)t]. Determine the following. %3D (a) amplitude of oscillation for the oscillating mass How does the amplitude of oscillation compare to the magnitude of the maximum displacement from equilibrium? m (b) force constant for the spring N/m (c) position of the mass after it has been oscillating for one half a period m (d) position of the mass one-third of a period after it has been released (e) time it takes the mass to get to the position x = -0.10 m after it has been releasedarrow_forward
- Suppose that you have a potential V (x) x2 + 6x – 8. Using a Taylor Series around Xo = 3, approximate the potential as a harmonic oscillator. O + (= – 3)? 7-2 (포-3)2 | (x – 3)? ||arrow_forwardUse the following transformation to solve the linear harmonic oscillator problem: Q = p + iaq, P = (p − iaq) / (2ia)arrow_forwardItem 1 Learning Goal: To understand the application of the general harmonic equation to the kinematics of a spring oscillator. One end of a spring with spring constant k is attached to the wall. The other end is attached to a block of mass m. The block rests on a frictionless horizontal surface. The equilibrium position of the left side of the block is defined to be x = 0. The length of the relaxed spring is L. (Figure 1) The block is slowly pulled from its equilibrium position to some position init> 0 along the x axis. At time t = 0, the block is released with zero initial velocity. The goal is to determine the position of the block (t) as a function of time in terms of w and init It is known that a general solution for the displacement from equilibrium of a harmonic oscillator is x(t) = C cos (wt) + S sin (wt), where C, S, and w are constants. (Figure 2) Your task, therefore, is to determine the values of C and S in terms of w and init Figure 1 of 3 L Xinit win x = 0 Part A Using the…arrow_forward
arrow_back_ios
arrow_forward_ios