Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
Bartleby Related Questions Icon

Related questions

Q: b. S dx cos2 x V9 + tan x
A: Using the substitution method and then find the given integration..... explanation of the solution…
Q: a. +4 cos x +6 sec x – 5 ) dx 2 x5
A:
Q: TT b) F /1- 1 – cos (2x) dx 2
A: Topic-Integration
Q: Evaluate √x² cos (2³) de dx
A: The given integral is: I=∫x2cosx3dx    ...1   As we know the common integral. ∫cosxdx=sinx+C And…
Q: 2. Find each of the following derivatives: d 1 dx x° ,5 d x (י4x+ nא1 (3sin ,3 dx d (7) .3 dx d [tan…
A:
Q: | w(w? + 1)3dw -1 dx х2 sin30cose d0
A: We will answer the first question since exact one wasn't specified, Please resubmit the question and…
Q: 1. Evaluate x + x? (y) dy dx. COS
A:
Q: Evaluate sin(9æ)cos(3x)dæ.
A:
Q: 3. Evaluate J,?-6x+5 1 dx if it exists. |
A:
Question
### Problem 1: Evaluate the Integral Consider the double integral: \[ \int_{0}^{1} \int_{-\sqrt{1-x^2}}^{0} 2x \cos \left( y - \frac{y^3}{3} \right) \, dy \, dx \] #### Explanation: This problem involves evaluating a double integral over a specified region. The inner integral is with respect to \( y \), ranging from \( -\sqrt{1-x^2} \) to \( 0 \). The outer integral is with respect to \( x \), ranging from \( 0 \) to \( 1 \). The integrand consists of the function \( 2x \cos \left( y - \frac{y^3}{3} \right) \), incorporating both the trigonometric cosine function and a cubic polynomial in \( y \). The problem likely requires utilizing integration techniques suitable for such functions, potentially involving substitution or numerical methods, depending on the context. #### Steps for Evaluation: 1. **Start with the inner integral**: Integrate \( 2x \cos \left( y - \frac{y^3}{3} \right) \) with respect to \( y \). 2. **Proceed to the outer integral**: Once the inner integration is performed, integrate the resulting expression with respect to \( x \). This problem illustrates a typical application of double integrals, emphasizing the importance of understanding the limits of integration and the integration techniques applicable to the given functions.
expand button
Transcribed Image Text:### Problem 1: Evaluate the Integral Consider the double integral: \[ \int_{0}^{1} \int_{-\sqrt{1-x^2}}^{0} 2x \cos \left( y - \frac{y^3}{3} \right) \, dy \, dx \] #### Explanation: This problem involves evaluating a double integral over a specified region. The inner integral is with respect to \( y \), ranging from \( -\sqrt{1-x^2} \) to \( 0 \). The outer integral is with respect to \( x \), ranging from \( 0 \) to \( 1 \). The integrand consists of the function \( 2x \cos \left( y - \frac{y^3}{3} \right) \), incorporating both the trigonometric cosine function and a cubic polynomial in \( y \). The problem likely requires utilizing integration techniques suitable for such functions, potentially involving substitution or numerical methods, depending on the context. #### Steps for Evaluation: 1. **Start with the inner integral**: Integrate \( 2x \cos \left( y - \frac{y^3}{3} \right) \) with respect to \( y \). 2. **Proceed to the outer integral**: Once the inner integration is performed, integrate the resulting expression with respect to \( x \). This problem illustrates a typical application of double integrals, emphasizing the importance of understanding the limits of integration and the integration techniques applicable to the given functions.
Expert Solution
Check Mark
Step 1: Description for the given question

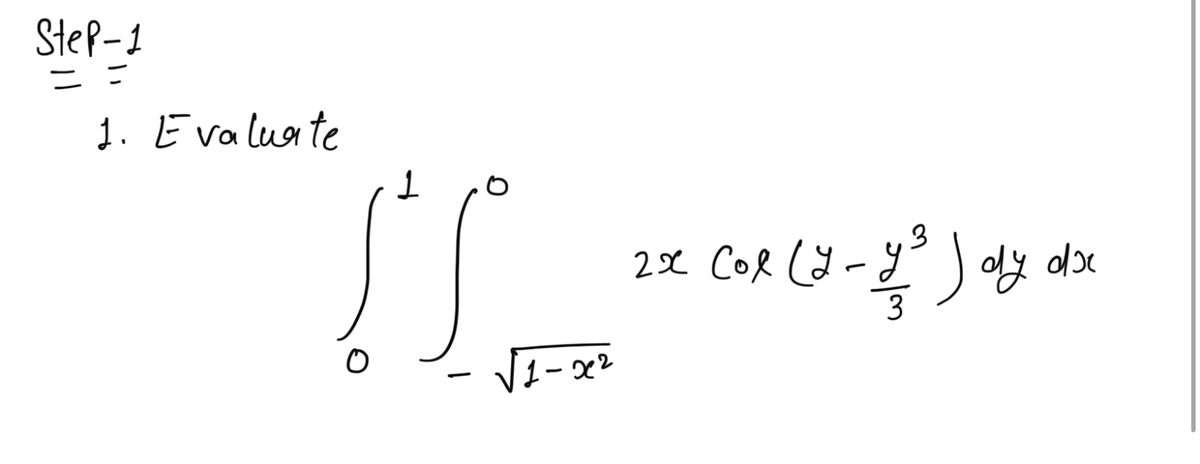
Calculus homework question answer, step 1, image 1

bartleby

Step by stepSolved in 4 steps with 4 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Similar questions
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS