1. Estimate the volume of the following solids by Riemann sums b) The solid lying above the rectangle R = [0,2] × [0, 4] and below f(x, y) X 2. Choose the Riemann sum such that m = n = 2 and choose the points to be evaluated as the upper right corner of each partial domain.
![1. Estimate the volume of the following solids by Riemann sums
b) The solid lying above the rectangle R = [0,2] × [0, 4] and below f(x, y)
12. Choose the Riemann sum such that m = n = 2 and choose the
points to be evaluated as the upper right corner of each partial domain.](/v2/_next/image?url=https%3A%2F%2Fcontent.bartleby.com%2Fqna-images%2Fquestion%2F526a6d9d-32b7-4f2d-90af-ff9540132ca2%2F92d2276c-f349-4b39-9e5c-d07761986654%2F6626hti_processed.jpeg&w=3840&q=75)
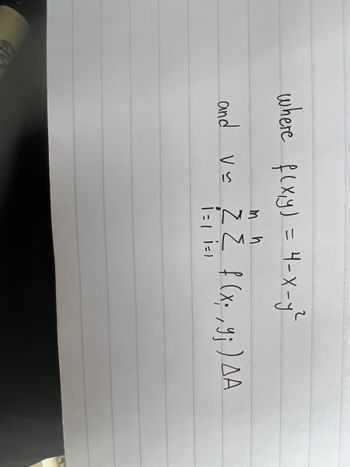
What is Riemann Sum:
The area under the graph of a positive function on an interval can be approximated by adding the areas of rectangles whose heights are defined by the curve in single-variable calculus. Typically, the interval was divided into smaller sub-intervals, rectangles were drawn to represent the area under the curve on each of these smaller sub-intervals, and the sum of these areas was used to indicate the area under the curve. This approach can be extended to the three-dimensional counterparts of double Riemann sums and double integrals over rectangles.
Given:
A solid is given that lies below and above the rectangle .
To Determine:
We determine the volume of the solid using upper left corner rule Riemann sum.
Step by step
Solved in 3 steps with 1 images
