1. A meter stick is balanced at its center. When you hang different mass blocks from different positions on the stick, as shown below, the stick remains balanced. Draw all forces exerted on the stick. Remember to include the force exerted by the Earth on the stick. Describe a rule that can be used show that the meter stick will remain balanced. 10 50 70 90 20 40 50 100 cm cm cm cm cm cm cm cm 100 g 100 g 100 g 100 g 200 g 10 50 100 10 50 60 cm cm cm ст cm cm d. 100 g 80 g 100 g 400 g Describe the rule you devised.
Angular speed, acceleration and displacement
Angular acceleration is defined as the rate of change in angular velocity with respect to time. It has both magnitude and direction. So, it is a vector quantity.
Angular Position
Before diving into angular position, one should understand the basics of position and its importance along with usage in day-to-day life. When one talks of position, it’s always relative with respect to some other object. For example, position of earth with respect to sun, position of school with respect to house, etc. Angular position is the rotational analogue of linear position.
Hello. Since your question has multiple sub-parts, we will solve first three sub-parts for you. If you want remaining sub-parts to be solved, then please resubmit the whole question and specify those sub-parts you want us to solve.
Answer:
a.
Consider the following figure which shows the all forces involved in the given situation.
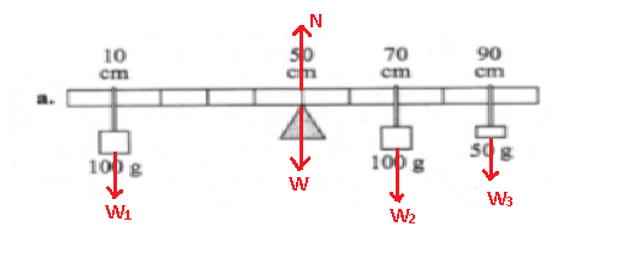
Here, W represents the weight of meter stick, N is the normal reaction force acting on the meter stick at the fulcrum or pivot, and W1, W2, and W3 are the weights suspended from the meter stick (see figure).
Now, we need to calculate the clockwise and anticlockwise moments due to the weights suspended from the rule about the center of the meter stick.
The clockwise moment is calculated in the following way.
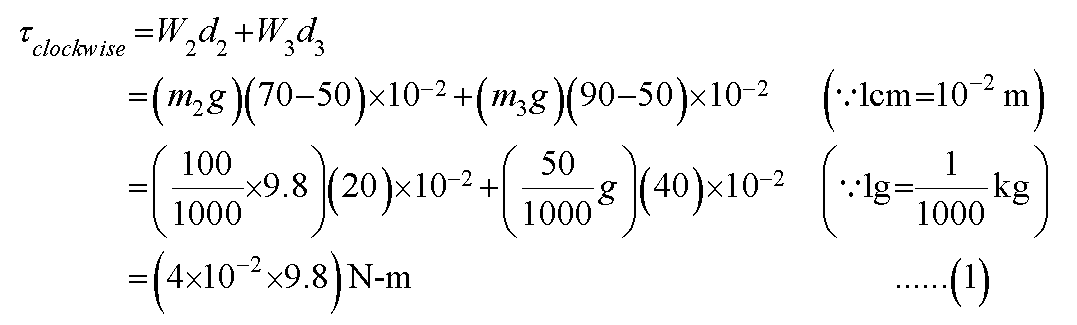
Here, m represent the mass and d represent the distance of the respective mass from the center of the meter stick.
The anticlockwise moment is calculated in the following way.
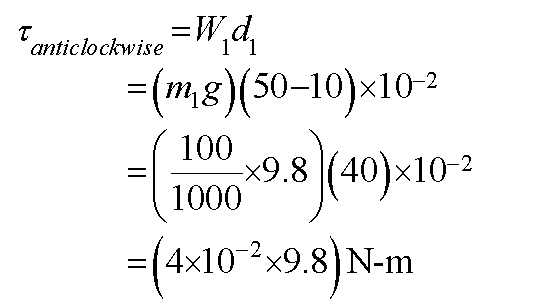
According to equations (1) and (2), it is evident that the total clockwise moment of the meter stick about the center of the rule is equal to the total anticlockwise moment of the meter rule about the center of the rule. This means that the net moment of the meter stick about the center is equal to zero. This is the condition of the equilibrium.
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 10 images
