1. A block of mass 1.71 kg is placed on a frictionless floor and initially pushed northward, whereupon it begins sliding with a constant speed of 3.50 m/s. It eventually collides with a second, stationary block, of mass 4.04 kg, head-on, and rebounds back to the south. The collision is 100% elastic. What will be the speeds of the 1.71-kg and 4.04-kg blocks, respectively, after this collision?
please answer all
1. A block of mass 1.71 kg is placed on a frictionless floor and initially pushed northward, whereupon it begins sliding with a constant speed of 3.50 m/s. It eventually collides with a second, stationary block, of mass 4.04 kg, head-on, and rebounds back to the south. The collision is 100% elastic. What will be the speeds of the 1.71-kg and 4.04-kg blocks, respectively, after this collision?
2. Same situation as before. This time it s a block of mass 1.07 kg sliding with a constant velocity of 3.51 m/s to the north, which collides 100% elastically with a second, stationary block, of mass 4.28 kg, head-on, and rebounds back to the south, eventually colliding 100% elastically with a wall and rebounding northward. It then overtakes the second block, which is still moving north as a result of the first collision. What will be the speeds of the 1.07-kg and 4.28-kg blocks, respectively, after their SECOND collision with one another?
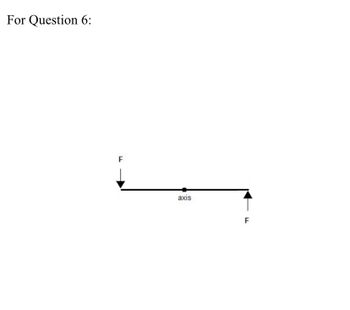
3. Consider a non-rotating space station in the shape of a long thin uniform rod of mass 6.07 x 10^6 kg and length 613 meters. Rocket motors on both ends of the rod are ignited, applying a constant force of F = 1.79 x 10^5 N to each end of the rod as shown in the diagram, causing the station to rotate about its center. If the motors are left running for 2 minutes and 39 seconds before shutting off, then how fast will the station be rotating when the engines stop? (attached is the diagram for this question)
Step by step
Solved in 3 steps
