Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: 7. Prove that the function f:Z → Z defined by f (x) = x + 8 is one-to-one and onto.
A:
Q: Let f(z) be an entire function satisfying that f(z)| ≤|z² for all z. Show that f(z) = az² for some…
A:
Q: 1. Let f : Z6 → Z6 be such that f(7) = x2 + 3. (a) Is f a well defined function? (b) Is f…
A: Since you have posted a question with multiple sub-parts, we will solve first three sub parts for…
Q: prove that The function f : R → R defined by f (x) = 3x − 5 is onto and one to one
A:
Q: g(x) = e2" + x² – 2 with R>0 - 2²
A:
Q: 5. Prove that the function f: Z → Z defined by f(x) = 3x + 1 is one-to-one.
A:
Q: Suppose I is an open interval (a, b) and f is a function defined on I which is strictly monotone…
A: Suppose I is an open interval (a, b) and f is a function defined on I which is strictly monotone…
Q: Let f (x) = x + x3 + 2x 1. The function f is increasing on the following interval(s): (а, b) O [a,…
A:
Q: Let F be the set of all functions of the form f : N {0, 1}. Also, let G be the set of all functions…
A: We have to find all possible options that are correct for the given question.
Q: Suppose f: Z → Z is defined by f = {(x,4x + 5):x € Z}. Determine the domain, codomain and range of…
A: Suppose f: z → z  is defined by         f = {  (x, 4x+5)  :  ∈z}        or    f(x) = 4x+5 : x∈z…
Q: Let g : B → N × N where B C Z given by g(m) = (|m| + 2, |m| + 3). Choose all subsets B such that g…
A:
Q: 22
A:
Q: 1. Give an example of a function f N N which is injective but not surjective.
A:
Q: Determine L[f]if 0, f(1) = {1- 1, 0 2. 1,
A: Given that, A function f(t), t ≥ 0, its Laplace transform F(s) = L{f(t)} is defined as
Q: Determine b so that f(x) is continuous if O 8 x + 6 xS 6 f( x ) = D O 2 x2 + bx +10 x > 6 b =
A:
Q: (1) Let f be a function from A to B, {An} a sequence of subsets of A, and {B} a sequence of subsets…
A:
Q: 5. Let f be defined by the floor function f(x) = [] and let S = {-3, -2, -1, 0, 1, 2, 3}. a)…
A:
Q: 1. Define function f : Z+ → Z such that f(n) = /n. (a) Is f one-to-one? Justify (prove) your answer.
A:
Q: Suppose f: R → R is a function defined by f(x) = x³. (a) Find f([-1,1]) and f-¹([0, 8]). (b) Show…
A: We shall use the intermediate value theorem to answer this question
Q: Let g: RxR → RxR be a function defined by g(x, y) = (x², x-y). Suppose that X = Rx{0} and D= {(a, a)…
A: Bartleby Guideline : ''Since you have posted a question with multiple sub parts , we will provide…
Q: 3. (a) Let f: X → Y and g: Y→ Z be functions. Prove the following statements. If f and g are both…
A: We can prove the following parts .
Q: 3. The function f(m, n) = 2"3" is a one-to-one function from N x N into N. (a) Calculate f(m, n) for…
A:
Q: O Find the largest value of A such that the function f(x) = x + 1x? - 4x + 6 is decreasing for all x…
A:
Q: Use the mathematical definition of concave and quasi-concave functions to prove that: 3. (a) The sum…
A: A real-valued function f {\displaystyle f} on an…
Q: 3. Please help!!: Calculate the domain of the function
A: If you have any questions let me know in comment box thankyou for your question.
Q: 2 (a) Prove that, if a and b are nonnegative integers such that a 4 b, then 3ª = 3. (b) Using (a),…
A: Given a, b are non negative integers such that a≡4b . Then to show 3a≡53b. To show the function…
Q: (n) If A is a subset of the codomain of f, explain why f(f-1(A)) is a subset of A. (0) Give an…
A: The functions have a property that if x∈Domain of f(x), then, the value of f(x) will be  unique,…
Q: D. Let function g: R → R be defined by g(x) = 2x + 1 5 cx in its domain. Why does your choice of c…
A:
Q: function g : Z → Z is defined as g(n) = |n| + 1. Show that this function is not injective and not…
A:
Question
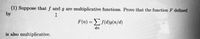
(1) Suppose that f and g are multiplicative functions. Prove that the function F defined by F(n) = f(d)g(n/d) d|n is also multiplicative.
expand button
Transcribed Image Text:(1) Suppose that f and g are multiplicative functions. Prove that the function F defined by F(n) = f(d)g(n/d) d|n is also multiplicative.
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
See solutionCheck out a sample Q&A here
Step 1
VIEW
Step 2
VIEW
bartleby

Step by stepSolved in 2 steps

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS