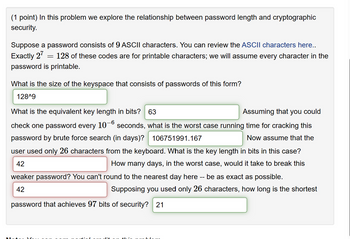
(1 point) In this problem we explore the relationship between password length and cryptographic security. Suppose a password consists of 9 ASCII characters. You can review the ASCII characters here.. Exactly 27 = 128 of these codes are for printable characters; we will assume every character in the password is printable. What is the size of the keyspace that consists of passwords of this form? 128^9 What is the equivalent key length in bits? 63 Assuming that you could check one password every 10-6 seconds, what is the worst case running time for cracking this password by brute force search (in days)? 106751991.167 Now assume that the user used only 26 characters from the keyboard. What is the key length in bits in this case? How many days, in the worst case, would it take to break this 42 weaker password? You can't round to the nearest day here be as exact as possible. 42 -- Supposing you used only 26 characters, how long is the shortest password that achieves 97 bits of security? 21

A: Solution:      Going by the first law, since the observation is that the house is next to the lake,…

A: We are given an equation for the line of best fit as,

A: The expected value of obtaining complete and accurate information about the state of nature before…

A:

A:

A:

A: Note- Since you have asked multiple question, we will solve the first question for you. If you want…

A: Recall the following facts.

A: We want to find ϕ(24)

A: We have to find integral of the given function, here we use formula for integrating the polynomials.

A:

A: We have to explain the steps.