
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
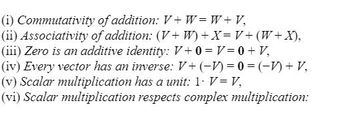
Transcribed Image Text:(i) Commutativity
of addition: V+W=W+V,
(ii) Associativity of addition: (V+W) + X = V + (W + X),
(iii) Zero is an additive identity: V+ 0 = V = 0 + V,
(iv) Every vector has an inverse: V+ (-1) = 0 =(-1) + V,
(v) Scalar multiplication has a unit: 1. V = V,
(vi) Scalar multiplication respects complex multiplication:

Transcribed Image Text:Exercise 2.2.3 Let c₁=2i, c₂ = 1+2i, and A =
1-i
2+2i
3
4+i
Verify Properties (vi) and (viii) in showing
2x2
is a complex vector space.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 3 steps with 2 images

Knowledge Booster
Similar questions
- 28. Is C a real vector space? Explain.arrow_forwardDetermine if the vector product <A,B> = a0b0 defines a valid inner product on P2(R) for any A=a0+a1x+a2x^2 and B=b0+b1X+b2x2. Explain your answer clearly.arrow_forwardLet S be the parallelogram then determine the area of parallelogram by the vectors [h | 1 and let A = h and [0 h+1] h=102 Also compute the area of the image of parallelogram under the linear transformation ""arrow_forward
- 7. Find the coordinates of the vector v relative to the ordered basis B. a) B = {x² + 2x + 2, 2x + 3,−x² + x + 1} v=-3x² + 6x + 8 14 D b) B = {[1₁¹] [ = (₁ 3²1 -CAC) = B₂ -QAED = 0 v= c) B₁ v= 22arrow_forwardDon't use chat gptarrow_forward"On R², define the operations of addition and scalar multiplication as follows: (X₁, X₂) + (y₁ Y₂) = (x₂ + y₂ +1, x₂ + y₂ + 1), c(x₁, x₂) = (Cx₂ + C-1, ₂+c-1). Then R² with these operations forms a vector space." Note that here the zero vector is (-1,-1) and the additive inverse of (x1, x2) is (-X₁-2, -x₂-2), not (-x₂-x₂)- a) Show that (-1, -1) acts as the zero vector under these definitions.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

