
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
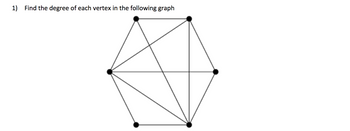
Transcribed Image Text:**Graph Exercise:**
1) **Problem Statement:** Find the degree of each vertex in the following graph.
**Graph Description:**
The graph displayed consists of seven vertices, forming a hexagon with an additional central vertex. The vertices are connected as follows:
- Each vertex of the hexagon is connected to the two adjacent vertices, forming the outer hexagon.
- The central vertex is connected to each of the vertices of the hexagon.
- Additional lines connect some vertices in the hexagon directly across, forming an internal star-like pattern within the hexagon.
**Degree of Vertices:**
To solve the exercise, you need to count the number of edges connected to each vertex.
- **Outer Hexagon Vertices:** Each of these vertices is connected to three other vertices in the pattern (two adjacent vertices plus the central vertex).
- **Central Vertex:** This vertex is connected to all six vertices of the hexagon.
Understanding these connections will allow you to determine the degree for each vertex in the graph.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 2 steps with 2 images

Knowledge Booster
Similar questions
- find each of the following on the graph: odd vertex, even vertex, bridge, loop, circuit, vertex of degree 5.arrow_forwardSuppose a pail holds 12 quarts of water, the two jars hold 7 quarts and 5 quarts, and the goal is still to split the water evenly with 6 quarts in both the pail and the larger jar. Produce a complete graph model for this puzzle, and find all solutions to the water puzzle in terms of the properties of the graph.arrow_forwardIf the graph G has exactly three components, then the number of components of K| UG isarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

