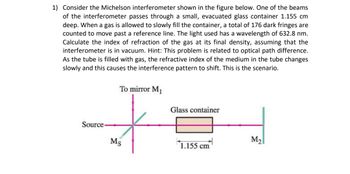
1) Consider the Michelson interferometer shown in the figure below. One of the beams of the interferometer passes through a small, evacuated glass container 1.155 cm deep. When a gas is allowed to slowly fill the container, a total of 176 dark fringes are counted to move past a reference line. The light used has a wavelength of 632.8 nm. Calculate the index of refraction of the gas at its final density, assuming that the interferometer is in vacuum. Hint: This problem is related to optical path difference. As the tube is filled with gas, the refractive index of the medium in the tube changes slowly and this causes the interference pattern to shift. This is the scenario. To mirror M₁ Glass container Source Ms M2 1.155 cm

MY NOTES ASK YOUR TEACHER PRACTICE ANOTHER A 2000 Hz sound wave passes through a wall with two narrow openings 30 cm apart. If sound travels on average 355 m/s, find the following. (a) What is the angle of the first order maximum? 36.27 (b) Find the slit separation when you replace the sound wave with a 2.30 cm microwave, and the angle of the first order maximum remains unchanged. 3.8878 How do you find the angle of a diffraction pattern, given wavelength? m (c) If the slit separation is 1.00 µm, what frequency of light gives the same first order maximum angle? 6.0007e-8X How do you find the angle of a diffraction pattern, given wavelength? Hz Additional Materials O Reading

Problem 5:   Light of wavelength λ = 450 nm passes through a single slit of width a = 0.32 mm. A diffraction pattern is formed on a screen L = 1.2 m away. Part (a)  Express the relative intensity, I/Imax, of the light at an angle θ in terms of θ, a and λ.  Part (b)  Calculate the value of I/Imax at an angle of θ = 28°.

1) A screen that is 1.0m wide is 2.0m away from a pair of slits illuminated by 633-nmlight, with the screen centered between the slits. Find the highest-order brightfringe that will appear on the screen if the slit spacing is (a) 0.10mm and (b)10µm.

3. A particular diffraction grating has 1 300 grooves per millimeter, and 15.0 mm of illuminated area. a) Assuming an incident angle of 45.0°, calculate the diffraction angle for first-order light at 625 nm. b) What wavelength of light would give this same diffraction angle in the second order? )What is the first-order resolving power of the grating? d) What must be the separation (in nm) of two first-order spectral lines centered at 625 nm if they are to be resolved? e) What is the angular dispersion (in degrees) between the two lines in part (d) asthey emerge from the grating?

Question 3: Plane waves of light of wavelength 610 nm are incident on a single slit of width 75 μm. A lens focuses the plane waves on a screen 120 cm away (Fig. 2). (a) What is the width of the central maximum on the screen? (b) What is the intensity ratio between the central maximum and the first-order maximum? Light 120 cm Copyright © 2005 Pearson Prentice Hall, Inc. Figure 2

3. In a double slit experiment, the distance between the slits is d=1 mm. A screen is situated at a distance of 2.5 m from the slits. Point P is at a distance of 25 cm from O', as in Figure. O' is the orthogonal projection of the center between the slits (0) on the screen. Monochromatic light with frequency v= 550 THz is used in this experiment. (a) Calculate the intensity of light at point P. (b) Calculate the angle ZP00'. (c) Calculate the location of the first three maxima with respect to point O'. (d) Calculate the location of the first three minima with respect to point O'. BONUS: You now consider that each slit has width a =0.05 mm. Calculate the intensity of light at point P. P.

Entoptic halos. If someone looks at a bright outdoor lamp in otherwise dark surroundings, the lamp appears to be surrounded by bright and dark rings (hence halos) that are actually a circular diffraction pattern , with the central maximum overlapping the direct light from the lamp. The diffraction is produced by structures within the cornea or lens of the eye (hence entoptic). If the lamp is monochromatic at wavelength 550 nm and the first dark ring subtends angular diameter 2.5° in the observer’s view, what is the (linear) diameter of the structure producing the diffraction?