1 ,2
Q: In the Marvel comics universe, Quicksilver is awfully fast. Let's say he can run at a velocity of…
A: Since Quicksilver can run at a velocity of 0.56c, we can use the Lorentz factor to determine how…
Q: Suppose a rocket starts from rest on Earth (frame S) and accelerates at a rate of 1000 m/sec² (as…
A: To solve this problem, we can use the principles of special relativity. We can start by calculating…
Q: what is the time interval between the flashes?
A: Part (d) Given: The distance at which big flash occurs is x1=1390 m. The time interval of flashes…
Q: In the laboratory inertial frame, which we assume to be inertial, two events occur simultaneously at…
A: Given data: Δx= 3 m & Δt=10-8 sTo Calculate: Spatial Distance(Δx')
Q: A spaceship travels at 0.79c, where c is the speed of light. The journey takes 2 years according to…
A:
Q: Recall, from this chapter, that the factor gamma (γ) governs both time dilation and length…
A:
Q: An observer in reference frame S claims that two events occur simultaneously. As this observer sees…
A: Given data- An observer in reference frame S claims two events occur simultaneously- Event A point…
Q: The factor y (gamma) appears throughout the expressions of special relativity. It depends only on…
A:
Q: Recall, from this chapter, that the factor gamma (γ) governs both time dilation and length…
A: The original time,
Q: A light flashes at position x = 0 m. One microsecond later, a light flashes at position x = 1000 m.…
A: In first reference frame S, Spatial interval of the event, ∆x=1000 m-0 m =1000 m Temporal…
Q: A plane has lights on its nose and tail which are set to flash every 3 seconds (in the plane's frame…
A: Given,Lets take the flashing of light at the nose and tail as 2 events A and B respectively.The two…
Q: A new particle, the aarnion, has just been discovered! Careful measurements show that the aarnion…
A: GivenThe aarnion has an average lifetime (at rest), τ= 87 nsDistance tavelled by aarnion, d=24 m
Q: The elementary particle called a muon is unstable and decays in about 2.20μs, as observed in its…
A:
Q: Recall, from this chapter, that the factor gamma (γ) governs both time dilation and length…
A:
Q: George Gamow imagined a world in which the speed of light is only c = 10 mph (4.5 m/s), sothat…
A: The objective of this question is to understand the concept of relativistic effects and how they…
Q: Physics A wormhole is created, with one mouth stationary here on Earth, and the other mouth on…
A:
Q: A picture on the wall has dimensions of H x W inches. How fast does a moving observer need to go for…
A:
Q: A certain line in the spectrum of the light from a nebula has a wavelength of 656 nm instead of the…
A: Original wavelength of Nebula is given as, λ = 434 nm The wavelength of Nebula observed in…
Q: Any process used to keep time will appear to happen more slowly in a moving object, when seen by an…
A: Option 1st and 3rd are correct option. Option 1 - Any process used to keep time will appear to…
Q: Observers in reference frame S see an explosion located at x1= 480 m. Asecond explosion occurs 5μs…
A:
Q: 26.2) Estimate the total food energy needed for the planet's population assuming a diet of 2400…
A: The world population is P=7,800,000,000Amount of calories intake per day per personQ=2400…
Q: Two rockets are each 1800 m long in their rest frame. Rocket Orion, traveling at 0.80c relative to…
A: Let S be the earth's frame and S' be the rocket Sirius's reference frame. S' moves relative to S…
Q: The formula for length contraction gives the length of an interval on a ruler moving with velocity v…
A: The objective of the question is to find out the fraction by which the length of a meter stick is…
Q: A spacecraft is moving past the earth at a constant speed of 0.60 times the speed of light. The…
A: Given: Speed of spacecraft is v=0.60c. The time measured by astronaut is t0=3.2s.
Q: A moving spaceship measures 20m long, but according to an observer at rest looking at it, it seems…
A: Given value--- moving spaceship measures 20m long. an observer at rest looking at it, it seems to…
Q: Recall, from this chapter, that the factor gamma (γ) governs both time dilation and length…
A: Given,
Q: Question: Rod R₁ has a rest length of 1m and rod R₂ has a rest length of 2m. R₁ and R₂ are moving…
A: Given: Rod can be given as R1 and R2 Length is 2 m
Q: Problem 1: Show that the spacetime coordinates of an event seen in two reference frames moving at a…
A: Introduction: The theory of special relativity explains how space and time are linked for objects…
Q: In their common rest frame, two stars are 92.0 light-years (ly) apart. If they are 36.0 apart as…
A:
Q: A brick of mass 1kg travels to the right at 0.9c, where c is the speed of light. It collides with…
A: Write the relativistic expression for the momentum. p=mv1−v2c2 Here, m is the mass of the particle,…
Q: sible that in some fr
A: Given: An explanation is given as,
Q: An alien spaceship has a mass ofm= 3.2×109kg, and according to the crew, onboard the bow-to-stern…
A: mass of spaceship (m) = 3.2×109 kg Length measured onboard (Lo) = 680 m Length measured by…
Q: Recall, from this chapter, that the factor gamma (γ) governs both time dilation and length…
A: 0.1% of 1 kg be defined as, 0.001 kg. The energy released by conversion of mass 0.001 kg be given by…
Q: Chapter 37, Problem 006 Reference frame S' is to pass reference frame S at speed v along the common…
A: Solution: Given values, Time(∆ta)=14 svelocity(v)=0.99c
Q: Two spaceships are moving away from Earth in opposite directions, one at 0.83*c, and one at 0.83*c…
A:
Q: I need help on question 8?
A: Question no 8
Q: In the Marvel comics universe, Quicksilver is awfully fast. Let's say he can run at a velocity of…
A: A) Time measured by Quicksilver =distance measured by himHis speed =4.82 x 1050.75 x 3 x 108=0.0021…
Q: An observer in reference frame S claims that two events occur simultaneously. As this observer sees…
A:
Q: A particle has γ=18,399. a) Calculate c-v in m/s. (I would have asked for 1 - v/c, making the…
A: Given: a) γ=18,399 b) momentum, P = 1,739 MeV/c
Q: e Lorentz contraction formula in relativity theory relates the length L of an object moving at a…
A:
Q: An astronaut takes a light emitting beacon in a spaceship travelling at 0.87 c away from a…
A: Time dilation is the slowing down of a clock for an observer in relative motion w.r.t. to a…
Q: What is the velocity of an electron that has a momentum of 3.6 × 10-²¹kg. m/s? Electron mass is…
A:
recall from this chapter,that the factor gamma governs both time dilation and length contraction,where
when you multiply the time in moving frame by gamma,you get the longer(dilated) time in fixed fame.when you divide the length in moving frame by gamma,you get the shorter(contracted) length in your fixed frame.
Consider a high-speed rocket ship equipped with a flashing light source. If the frequency of flashes seen on an approaching ship is twice what it was when the ship was a fixed distance away, by how much is the period (time interval between flashes) changed? Is this period constant for a constant relative speed? For accelerated motion? Defend your answer.
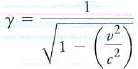
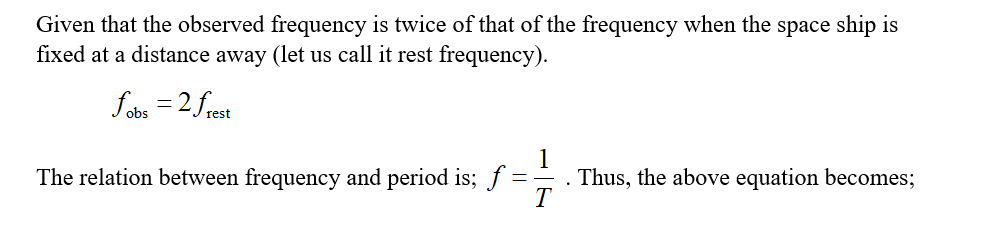
Trending now
This is a popular solution!
Step by step
Solved in 3 steps with 3 images
