Advanced Engineering Mathematics
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
Bartleby Related Questions Icon

Related questions

Q: 2 2. Find the eigenvalues and eigenvectors of the matrix A= -3 3 3 -4 -3 3 3 2 If A is…
A: The given matrix is The objective is to diagonalized the given matrix.First find the eigenvalues and…
Q: (2) Area of Triangle A=11* Of Triangle formed by V' and W in es =√6 A (11012) BC21014) ((|12₁k)|…
A:
Q: Hi, could you help me find the eigenvalues and eigenvectors of this matrix,
A: Given matrix To determine the Eigen values and Eigen vectors Using these formulas For Eigen values…
Q: 4 -2] find the eigenvalues and eigenvectors. 1 10. Given the matrix A =
A:
Q: The matrix -1 -57 A =|-5 10 3 -2 -7 has one real eigenvalue. Find this eigenvalue, its multiplicity,…
A: Here first we write characteristic equation of matrix, and then using characteristic equation we can…
Q: 3. Find the eigenvalues and eigenvectors of the matrix A = 0 3 3 7 3
A:
Q: Part 1: For the given matrix and eigenvalue, find an eigenvector corresponding to the eigenvalue.…
A:
Q: -2 2 Find the eigenvalues and eigenvectors of the matrix A 0 1 3 0 -4 d1 =, 51 = and and 13 v3
A:
Q: Q5) Given A = 0 – 2    4 determine if x = (1,1,0) is an eigenvector, why or why not?…
A: Note: Since you have asked multiple question, we will solve the first question for you. If you want…
Q: Find the eigenvalues of the matrix [4 0 A = 0 0 0 10 -3 For [1 2 3 A = 1 2 3 1 2 3 find one…
A:
Q: Sorry, this is the answer I calculated myself before. It marks as incorrect. Tried switching the…
A:
Q: Find both eigenvalues A₁ and A₂ and corresponding eigenvectors X₁ and X₂ of the matrix A= You MUST…
A: The given matrix is The characteristic equation of A is
Q: Problem 1: Solve the heat equation ut 5urz for a rod of length T with both ends insu- lated for all…
A:
Q: Find a 3 x 3 matrix A that has eigenvalues λ = 0, 12, -12, with corresponding eigenvectors DOO…
A: A  has eigenvalues , with the corresponding eigenvectorsThe aim is to find the matrix  that has the…
Q: 4) Eigen valves and eigenvectors Let's say A = 5 3 %3D A-AI = ]- 5. %3D 3. 5-2 L 30 ニ Quadratic…
A:
Q: A linear system x = Ax with state variables x₁(t) and a₂(t) is defined by the equations: *1 = 3x1…
A:
Q: Please solve the following by hand, have good detail and explain each part of the question step by…
A: image was blurr but i have tried my best to solve.
Q: Help me to solve it please
A:
Q: [3 0 07 6. Find the eigenvalues and eigenvectors of the matrix: 0 5 0 Lo 0 7.
A:
Q: (b) Find the fundamental matrix Þ(t) for the system x' = Ax which satisfies (0) = I. (c) Use Þ(t) to…
A:
Q: Please explain how I would find the eigenvectors of A = [3 1 0 2]. I know that the eigenvalues will…
A:
Q: (a) Find the eigenvalues of A. (b) Find two eigenvectors v and w of A with respect of the two…
A:
Q: Use the Newton method to solve the following system of equations using r= 2 and 0=0 as an initial…
A:
Q: Problem #3: Consider the following matrix A (whose 2nd and 3rd rows are not given), and vector x. A…
A:
Q: Q7. Find the eigenvalues 7 -9 18 (a) A = 0 -2 0 and associated eigenvectors for the given matrices.…
A: We have to find the eigen vector and eigen value of the matrix.
Question
100%

Hi this is a Linear Algebra question. I need help finding the Eigenvectors of the 3x3 matrix given that the Eigenvalues are 1 and 2. Please help me solve for 1 and 2 separately. Thank you in advance.

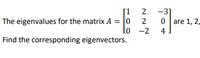
**Matrix Eigenvalue Problem** Given: The eigenvalues for the matrix \( A = \begin{bmatrix} 1 & 2 & -3 \\ 0 & 2 & 0 \\ 0 & -2 & 4 \end{bmatrix} \) are 1, 2, and 4. Task: Find the corresponding eigenvectors. To solve this, you would typically substitute each eigenvalue into the equation \( (A - \lambda I)x = 0 \) to find the eigenvectors \( x \). Here, \( \lambda \) represents an eigenvalue, and \( I \) is the identity matrix of the same dimension as \( A \).
expand button
Transcribed Image Text:**Matrix Eigenvalue Problem** Given: The eigenvalues for the matrix \( A = \begin{bmatrix} 1 & 2 & -3 \\ 0 & 2 & 0 \\ 0 & -2 & 4 \end{bmatrix} \) are 1, 2, and 4. Task: Find the corresponding eigenvectors. To solve this, you would typically substitute each eigenvalue into the equation \( (A - \lambda I)x = 0 \) to find the eigenvectors \( x \). Here, \( \lambda \) represents an eigenvalue, and \( I \) is the identity matrix of the same dimension as \( A \).
Expert Solution
Check Mark
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
See solutionCheck out a sample Q&A here
Step 1
VIEW
Step 2
VIEW
bartleby

Step by stepSolved in 2 steps with 2 images

See solution
Check out a sample Q&A here
Blurred answer
Knowledge Booster
Background pattern image
Advanced Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, advanced-math and related others by exploring similar questions and additional content below.
Similar questions
Recommended textbooks for you
Text book image
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Text book image
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Text book image
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Text book image
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,
Text book image
Basic Technical Mathematics
Advanced Math
ISBN:9780134437705
Author:Washington
Publisher:PEARSON
Text book image
Topology
Advanced Math
ISBN:9780134689517
Author:Munkres, James R.
Publisher:Pearson,
SEE MORE TEXTBOOKS