
Structural Analysis
6th Edition
ISBN: 9781337630931
Author: KASSIMALI, Aslam.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Determine the state of stress a point A on the cross section a-a, finding the normal and shear stress at A, when P=24kN.
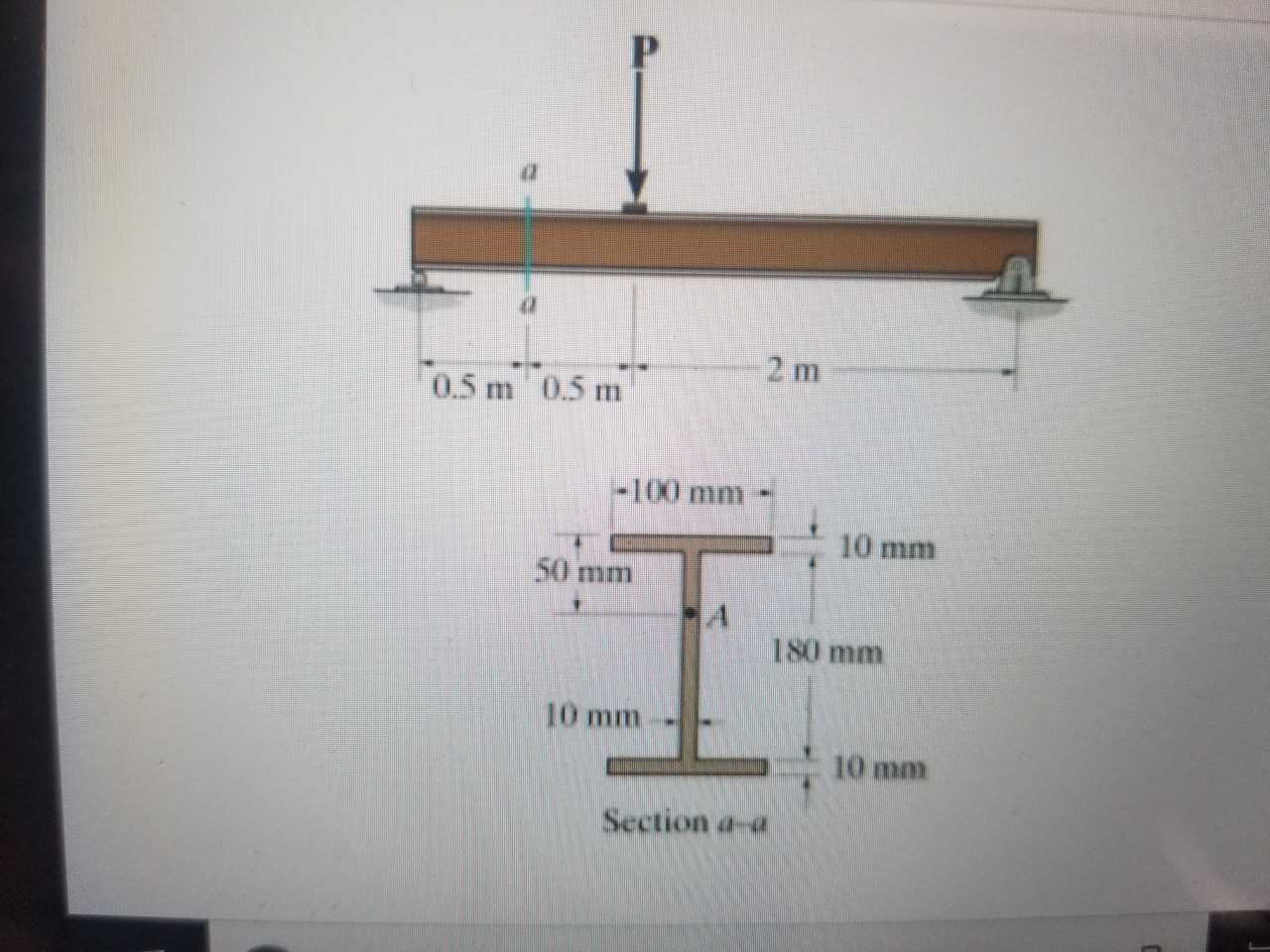
Transcribed Image Text:0.5 m 0.5 m
2 m
100 mm
50 mm10 mm
180 mm
10 m
10 mm
Section a-a
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 10 steps with 9 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.Similar questions
- Q-5: For the element with stresses as shown below, find: a. The magnitudes and directions of major and minor principal stresses b. The shear and normal stresses acting on a horizontal plane as shown below 8kPa 2kPa 75° 75° экра TH Jon OH 4kPa 30° Horizontal planearrow_forwardCylinder of height 2H. radius R. centroid at (0,0.H), axis e3 undergoes deformation x = o(z) = z + 23e3. Assuming stress-strain relation: S = aE, where a is a constant, total force on the base of the cylinder with normal -e3 is f = -1.5anR2 He3 total force on the base of the cylinder with normal - ez is f = 1.5aπR²e3 total force on the base of the cylinder with normal - ez is f = 1.5an R²Hez total force on the base of the cylinder with normal - ez is f = -1.5anR²e3arrow_forwardThe split ring shown has an inner radius ₁ = 0.8 in. and a circular cross section of diameter d= 0.6 in. Knowing that each of the 100-lb forces Pis applied at the centroid of the cross section, determine the stress at point A and at point B. P B The stress at point A is The stress at point B is P ksi. ksi.arrow_forward
- Q-2-dimensional fluid elements is subjected to hydrostatic pressure 20 MPa. The maximum shear stress (in MPa) at the point is..?arrow_forwardThe state of stress at a point is shown on the element. Enter your answers numerically separated by commas. ΥΠ ΑΣφ vec max min = ksi Submit Request Answer Figure Part B Determine the absolute maximum shear stress. ΑΣφ ve 2.5 ksi ksi Fabs mar= 4 ksi Submit Request Answer 5 ksi Provide Feedback 圓arrow_forwardPart 2,3,4arrow_forward
- Problem 5: The stresses on the x-y-axes are o, = 8 ksi, o, = 12 ksi, and Ty = -5 ksi. Draw the Mohr's circle for this stress state. Identify the maximum shear stress from the Mohr's circle, and draw the maximum shear stress element, specifying its orientation.arrow_forwardThe d = 16-mm-diameter solid rod passes through a D = 21-mm-diameter hole in the support plate. When a load P is applied to the rod, the rod head rests on the support plate. The support plate has a thickness of b = 11 mm. The rod head has a diameter of a = 32 mm, and the head has a thickness of t = 10 mm. The shear stress in the rod head cannot exceed 130 MPa, the punching shear stress in the support plate cannot exceed 90 MPa, and the bearing stress between the rod head and the support plate cannot exceed 145 MPa. Determine the maximum value of Pmax that can be supported by the structure. P Support Plate Rod Answer: Pmax i Hole diameter D Head KNarrow_forwardPlease use Mohr's Circle.arrow_forward
- 7-3. For the given state of stress shown, determine: (a) the principal stress, and (b) the maximum in-plane shear stress and the associated average normal stress. Also, for each case, determine thecorresponding orientation of the element with respect to the element shown, and sketch the results oneach element.arrow_forward8 Expansion is an axial deformation. 9 True 10 False The coordinates of centroid locate the ge ometric center of the cross-section of the material.( True False Torsional stress is also known as bending stress.( True Falsearrow_forwardAll forces applied in the system are in the (x - y) plane. The material point B at the top of the beam is rotated at an angle of 15° counterclockwise. It is required that the shear stress is 17.5 MPa for this rotated material point B. At the bottom point A of the beam it is required that the maximum tensile stress is 110 MPa. Determine the load P and the length d that satisfies these constraints defined for points A and B. Given data: L= 4 b, t = b / 25, c = 2b, b = 1000 mm, e = 12, f=5 b/4- q = 2P/L b/ 4 -b/4- Parrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you

 Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON
Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
 Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning


Structural Analysis (10th Edition)
Civil Engineering
ISBN:9780134610672
Author:Russell C. Hibbeler
Publisher:PEARSON

Principles of Foundation Engineering (MindTap Cou...
Civil Engineering
ISBN:9781337705028
Author:Braja M. Das, Nagaratnam Sivakugan
Publisher:Cengage Learning

Fundamentals of Structural Analysis
Civil Engineering
ISBN:9780073398006
Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel Lanning
Publisher:McGraw-Hill Education


Traffic and Highway Engineering
Civil Engineering
ISBN:9781305156241
Author:Garber, Nicholas J.
Publisher:Cengage Learning