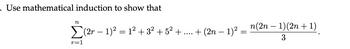
. Use mathematical induction to show that n Σ r=1 (2r − 1)² = 1² + 3² +5² + + (2n − 1)² = = n(2n − 1) (2n + 1) 3

4:28 AM Mon Mar 1 ll ? @ 10 Done AA A student.desmos.com = Aigebra 2: Operations w/... Merlanda Petit jacques 6 of 7 Next Polynomials #6 Simplify by multiplying. Show all of your work! Sub (n² + 6n – 4)(2n – 4)

(a) Find the eigenvalues and corresponding eigenvectors of the following matrix: 0-4 A = 05 -4 4 4 3 (b) The matrix A = ·( |has eigenvalues A₁ = -1 with eigenvector X₁ = [1, -2]T, and A₂ = -3 with eigenvector X₂ = [1,-1]T. 1 If P is a matrix such that P = ( X₁ X₂ ) = (-¹/₂2 - ₁1), s -1 gives a diagonal matrix with the same eigenvalues as A. -5-2 1 show that P-¹AP

8 For which values of mis x - 1 a factor of x³ + m²x² + 3mx + 1? (a) Show that n = 1 is a root of the p(n) = n³ − 8n² + 20n − 13. (b) Factor p(n). (c) For how many values of n is p(n) prime?