A First Course in Probability (10th Edition)
10th Edition
ISBN: 9780134753119
Author: Sheldon Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Related questions
Question
thumb_up100%
I need help with this please
![Two catalysts in a batch chemical process are being compared for their effect on the output of the process reaction. A
sample of 11 batches was prepared using catalyst 1 and gave an average yield of 94 with a sample standard deviation
of 4. A sample of 15 batches was prepared using catalyst 2 and gave an average yield of 89 and a sample standard
deviation of 5. Find a 99% confidence interval for the difference between the population means, assuming that the
populations are approximately normally distributed with equal variances.
Click here to view page 1 of the table of critical values of the t-distribution.
Click here to view page 2 of the table of critical values of the t-distribution.
Let μ₁ be the population mean for catalyst 1 and let μ₂ be the population mean for catalyst 2.
The confidence interval is ] < H₁ = H₂ < [
(Round to two decimal places as needed.)](https://content.bartleby.com/qna-images/question/60d60483-3b91-4b14-b6e0-d18f4cf37a4c/f91c82e9-fccb-4820-915d-152a9514c2d2/kri5vr_processed.png)
Transcribed Image Text:Two catalysts in a batch chemical process are being compared for their effect on the output of the process reaction. A
sample of 11 batches was prepared using catalyst 1 and gave an average yield of 94 with a sample standard deviation
of 4. A sample of 15 batches was prepared using catalyst 2 and gave an average yield of 89 and a sample standard
deviation of 5. Find a 99% confidence interval for the difference between the population means, assuming that the
populations are approximately normally distributed with equal variances.
Click here to view page 1 of the table of critical values of the t-distribution.
Click here to view page 2 of the table of critical values of the t-distribution.
Let μ₁ be the population mean for catalyst 1 and let μ₂ be the population mean for catalyst 2.
The confidence interval is ] < H₁ = H₂ < [
(Round to two decimal places as needed.)
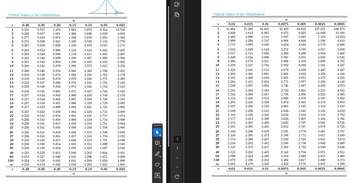
Transcribed Image Text:Critical Values of the t-Distribution
Critical Values of the t-Distribution
a
a
0.40
0.30
0.20
0.15
0.10
0.05
0.025
0.02
0.015
0.01
0.0075
0.005
0.0025
0.0005
1
0.325
0.727
1.376
1.963
3.078
6.314
12.706
1
15.894
21.205
31.821
42.433
63.656
127.321
636.578
2
0.289
0.617
1.061
1.386
1.886
2.920
4.303
2
4.849
5.643
6.965
8.073
9.925
14.089
31.600
3
0.277
0.584
0.978
1.250
1.638
2.353
3.182
3
3.482
3.896
4.541
5.047
5.841
7.453
12.924
4
0.271
0.569
0.941
1.190
1.533
2.132
2.776
4
2.999
3.298
3.747
4.088
4.604
5.598
8.610
5
0.267
0.559
0.920
1.156
1.476
2.015
2.571
5
2.757
3.003
3.365
3.634
4.032
4.773
6.869
в
0.265
0.553
0.906
1.134
1.440
1.943
2.447
6
2.612
2.829
3.143
3.372
3.707
4.317
5.959
7
0.263
0.549
0.896
1.119
1.415
1.895
2.365
7
2.517
2.715
2.998
3.203
3.499
4.029
5.408
8
0.262
0.546
0.889
1.108
1.397
1.860
2.306
8
2.449
2.634
2.896
3.085
3.355
3.833
5.041
9
0.261
0.543
0.883
1.100
1.383
1.833
2.262
9
2.398
2.574
2.821
2.998
3.250
3.690
4.781
10
0.260
0.542
0.879
1.093
1.372
1.812
2.228
10
2.359
2.527
2.764
2.932
3.169
3.581
4.587
11
0.260
0.540
0.876
1.088
1.363
1.796
2.201
11
2.328
2.491
2.718
2.879
3.106
3.497
4.437
12
0.259
0.539
0.873
1.083
1.356
1.782
2.179
12
2.303
2.461
2.681
2.836
3.055
3.428
4.318
13
0.259
0.538
0.870
1.079
1.350
1.771
2.160
13
2.282
2.436
2.650
2.801
3.012
3.372
4.221
14
0.258
0.537
0.868
1.076
1.345
1.761
2.145
14
2.264
2.415
2.624
2.771
2.977
3.326
4.140
15
0.258
0.536
0.866
1.074
1.341
1.753
2.131
15
2.249
2.397
2.602
2.746
2.947
3.286
4.073
16
0.258
0.535
0.865
1.071
1.337
1.746
2.120
16
2.235
2.382
2.583
2.724
2.921
3.252
4.015
17
0.257
0.534
0.863
1.069
1.333
1.740
2.110
17
2.224
2.368
2.567
2.706
2.898
3.222
3.965
18
0.257
0.534
0.862
1.067
1.330
1.734
2.101
18
2.214
2.356
2.552
2.689
2.878
3.197
3.922
19
0.257
0.533
0.861
1.066
1.328
1.729
2.093
2.205
2.346
2.539
2.674
2.861
3.174
3.883
20
0.257
0.533
0.860
1.064
1.325
1.725
2.086
20
2.197
2.336
2.528
2.661
2.845
3.153
3.850
21
0.257
0.532
0.859
1.063
1.323
1.721
2.080
21
2.189
2.328
2.518
2.649
2.831
3.135
3.819
22
0.256
0.532
0.858
1.061
1.321
1.717
2.074
22
2.183
2.320
2.508
2.639
2.819
3.119
3.792
23
0.256
0.532
0.858
1.060
1.319
1.714
2.069
23
2.177
2.313
2.500
2.629
2.807
3.104
3.768
24
0.256
0.531
0.857
1.059
1.318
1.711
2.064
24
2.172
2.307
2.492
2.620
2.797
3.091
3.745
25
0.256
0.531
0.856
1.058
1.316
1.708
2.060
25
2.167
2.301
2.485
2.612
2.787
3.078
3.725
26
0.256
0.531
0.856
1.058
1.315
1.706
2.056
27
0.256
0.531
0.855
1.057
1.314
1.703
2.052
28
0.256
0.530
0.855
1.056
1.313
1.701
2.048
-
29
0.256
0.530
0.854
1.055
1.311
1.699
2.045
30
0.256
0.530
0.854
1.055
1.310
1.697
2.042
40
0.255
0.529
0.851
1.050
1.303
1.684
2.021
60
0.254
0.527
0.848
1.045
1.296
1.671
2.000
120
0.254
0.526
0.845
1.041
1.289
1.658
1.980
8"
0.253
0.524
0.842
1.036
1.282
1.645
1.960
e
0.40
0.30
0.20
0.15
0.10
- <>
120
888 988
26
2.162
2.296
2.479
2.605
2.779
3.067
3.707
27
2.158
2.291
2.473
2.598
2.771
3.057
3.689
28
2.154
2.286
2.467
2.592
2.763
3.047
3.674
2.150
2.282
2.462
2.586
2.756
3.038
3.660
30
2.147
2.278
2.457
2.581
2.750
3.030
3.646
40
2.123
2.250
2.423
2.542
2.704
2.971
3.551
60
2.099
2.223
2.390
2.504
2.660
2.915
3.460
2.076
2.196
2.358
2.468
2.617
2.860
3.373
2.054
2.170
2.326
2.432
2.576
2.807
3.290
0.05
0.025
0.02
0.015
0.01
0.0075
0.005
0.0025
0.0005
a
A
a
C
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 1 images
Knowledge Booster
Similar questions
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- A First Course in Probability (10th Edition)ProbabilityISBN:9780134753119Author:Sheldon RossPublisher:PEARSON
A First Course in Probability (10th Edition)
Probability
ISBN:9780134753119
Author:Sheldon Ross
Publisher:PEARSON