Homework Help is Here – Start Your Trial Now!
Math
Advanced Math
The optimal solution of this linear programming problem is at the intersection of constraints 1 and 2. Max    3x1 + x2 s.t.               4x1 + x2 ≤ 400   4x1 + 3x2 ≤ 600   x1 + 2x2 ≤ 300   x1, x2 ≥ 0 Over what range can the coefficient of x1 vary before the current solution is no longer optimal? (Round your answers to two decimal places.) Over what range can the coefficient of x2 vary before the current solution is no longer optimal? (Round your answers to two decimal places.) Compute the dual value for the first constraint? Compute the dual value for the second constraint? Compute the dual value for the third constraint?

The optimal solution of this linear programming problem is at the intersection of constraints 1 and 2. Max    3x1 + x2 s.t.               4x1 + x2 ≤ 400   4x1 + 3x2 ≤ 600   x1 + 2x2 ≤ 300   x1, x2 ≥ 0 Over what range can the coefficient of x1 vary before the current solution is no longer optimal? (Round your answers to two decimal places.) Over what range can the coefficient of x2 vary before the current solution is no longer optimal? (Round your answers to two decimal places.) Compute the dual value for the first constraint? Compute the dual value for the second constraint? Compute the dual value for the third constraint?

College Algebra (MindTap Course List)
College Algebra (MindTap Course List)
12th Edition
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:R. David Gustafson, Jeff Hughes
Chapter6: Linear Systems
Section6.CR: Chapter Review
Problem 70E: A company manufactures two fertilizers, x and y. Each 50-pound bag of fertilizer requires three...
See similar textbooks
icon
Related questions
Question
The optimal solution of this linear programming problem is at the intersection of constraints 1 and 2.
Max    3x1 + x2
s.t.            
  4x1 + x2 ≤ 400
  4x1 + 3x2 ≤ 600
  x1 + 2x2 ≤ 300
  x1, x2 ≥ 0

Over what range can the coefficient of x1 vary before the current solution is no longer optimal? (Round your answers to two decimal places.)

Over what range can the coefficient of x2 vary before the current solution is no longer optimal? (Round your answers to two decimal places.)

Compute the dual value for the first constraint?

Compute the dual value for the second constraint?

Compute the dual value for the third constraint?

Expert Solution
trending now

Trending now

This is a popular solution!

steps

Step by step

Solved in 5 steps with 4 images

SEE SOLUTIONCheck out a sample Q&A here
Blurred answer
Follow-up Questions
Read through expert solutions to related follow-up questions below.
Follow-up Question

need correct answers. The ones here are incorrect

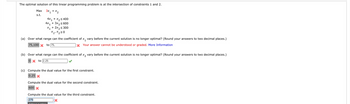
The optimal solution of this linear programming problem is at the intersection of constraints 1 and 2. Max 3x₁ + x₂ s.t. 4x₁ + x₂ ≤ 400 4x₁ + 3x₂ ≤600 X₁ + 2x₂ ≤ 300 X1 X₂20 (a) Over what range can the coefficient of x₁ vary before the current solution is no longer optimal? (Round your answers to two decimal places.) to 75, x Your answer cannot be understood or graded. More Information 75,100 (b) Over what range can the coefficient of x₂ vary before the current solution is no longer optimal? (Round your answers to two decimal places.) 0x to 2.25 (c) Compute the dual value for the first constraint. 0.25 X Compute the dual value for the second constraint. 600 X Compute the dual value for the third constraint. 275
Transcribed Image Text:The optimal solution of this linear programming problem is at the intersection of constraints 1 and 2. Max 3x₁ + x₂ s.t. 4x₁ + x₂ ≤ 400 4x₁ + 3x₂ ≤600 X₁ + 2x₂ ≤ 300 X1 X₂20 (a) Over what range can the coefficient of x₁ vary before the current solution is no longer optimal? (Round your answers to two decimal places.) to 75, x Your answer cannot be understood or graded. More Information 75,100 (b) Over what range can the coefficient of x₂ vary before the current solution is no longer optimal? (Round your answers to two decimal places.) 0x to 2.25 (c) Compute the dual value for the first constraint. 0.25 X Compute the dual value for the second constraint. 600 X Compute the dual value for the third constraint. 275
Solution
Bartleby Expert
SEE SOLUTION
Recommended textbooks for you
College Algebra (MindTap Course List)
College Algebra (MindTap Course List)
Algebra
ISBN:
9781305652231
Author:
R. David Gustafson, Jeff Hughes
Publisher:
Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:
9781305658004
Author:
Ron Larson
Publisher:
Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:
9781133382119
Author:
Swokowski
Publisher:
Cengage
Glencoe Algebra 1, Student Edition, 9780079039897…
Glencoe Algebra 1, Student Edition, 9780079039897…
Algebra
ISBN:
9780079039897
Author:
Carter
Publisher:
McGraw Hill
SEE MORE TEXTBOOKS