
Structural Analysis
6th Edition
ISBN: 9781337630931
Author: KASSIMALI, Aslam.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Question
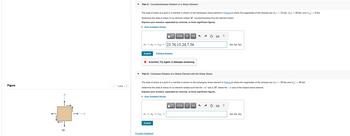
Transcribed Image Text:Figure
(a)
y
1 of 6
Part C - Counterclockwise Rotation of a Stress Element
The state of stress at a point in a member is shown on the rectangular stress element in (Figure 5) where the magnitudes of the stresses are |σ| = 10 ksi, |σy| = 29 ksi, and |7zy | = 6 ksi.
Determine the state of stress on an element rotated 40° counterclockwise from the element shown.
Express your answers, separated by commas, to three significant figures.
▸ View Available Hint(s)
ΕΧΕΙ ΑΣΦ
↓↑ vec
σ =σy = Ta'y = 23.76, 15.24,7.56
Submit
Previous Answers
× Incorrect; Try Again; 5 attempts remaining
Part D - Clockwise Rotation of a Stress Element with No Shear Stress
?
ksi, ksi, ksi
The state of stress at a point in a member is shown on the rectangular stress element in (Figure 6) where the magnitudes of the stresses are |σ| = 29 ksi and |σy| = 26 ksi.
Determine the state of stress on an element rotated such that the +x axis is 20° below the x axis of the original stress element.
Express your answers, separated by commas, to three significant figures.
▸ View Available Hint(s)
ΕΠΙ ΑΣΦ
↓↑ vec
σ = σy' = Tz'y' =
Submit
Provide Feedback
?
ksi, ksi, ksi
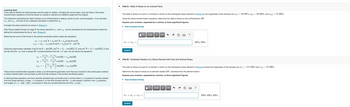
Transcribed Image Text:Part A - State of Stress on an Inclined Plane
Learning Goal:
To be able to identify the initial stresses and the angle of rotation, including the correct signs, and use these in the stress-
transformation equations to find the stress on a plane or element at a different angle than the original.
The method of calculating the state of stress on an inclined plane is tedious, prone to error, and incomplete--if we calculate
σ and Tz'y', we have to do a separate calculation to determine σy.
Consider the stress element (a) shown in (Figure 1).
After being rotated through an angle 0, the stress elements σ and Tr'y' can be calculated by the inclined-plane method by
letting the inclined plane be the y' axis. (Figure 2)
Balancing the sums of the forces in the primed coordinate system yields two equations:
σ =σ cos² +σy sin² 0 + Try (2 sin cos 0)
Try (σyσ) sin 0 cos 0+ Tzy (cos2 0 - sin2 0)
Using the trigonometric identities 2 sin 0 cos 0 = sin(20), sin² 0 = (1 - cos(20))/2, and cos² 0 = (1 + cos(20))/2 and
the fact that the +y' axis is always 90° counterclockwise from the +x axis, we can derive the equations:
The state of stress at a point in a member is shown on the rectangular stress element in (Figure 3); the magnitudes of the stresses are |σ| = 92 MPa, |oy| = 39 MPa, and |Tzy| = 57 MPa.
Using the stress-transformation equations, determine the state of stress on the inclined plane AB.
Express your answers, separated by a comma, to three significant figures.
▸ View Available Hint(s)
σ =, Tx'y' =
Submit
ΜΕ ΑΣΦ
vec
?
MPa, MPa
σ =
2
2
+ cos(20) + Tzy sin(20)
Oxtoy
στον
2
Oy =
Tz'y =
2
στ
cos(20) Tzy sin(20)
Jay) sin(20) + Try Cos(20)
2
These stress-transformation equations allow us to eliminate the geometric work that was involved in the incline-plane method
of stress transformation and provides us with all three stresses in the primed coordinate system.
In deriving these equations, we have used the standard sign convention that a normal stress, σ, is positive if it points outward
from the stress element, a shear, T, is positive if, on the face through with the +x axis passes, it points in the +y direction,
and angles, (-180°, 180°), are positive if they are counterclockwise from the +x axis.
Part B - Clockwise Rotation of a Stress Element with Only One Normal Stress
The state of stress at a point in a member is shown on the rectangular stress element in (Figure 4) where the magnitudes of the stresses are |σ| = 171 MPa and |Try | = 57 MPa.
Determine the state of stress on an element rotated 100° clockwise from the element shown.
Express your answers, separated by commas, to three significant figures.
View Available Hint(s)
σ =, σy' =, Tz'y' =
Submit
ΜΕ ΑΣΦ
↓↑
vec
?
MPa, MPa, MPa
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps

Knowledge Booster
Similar questions
- . The biaxial stress system in an element is shown in the figure. Which of the following will give the normal stress in N/mm2 in the plane BD making an angle of 45° with the plane BA? 2 0₁ = 60 N/mm² C 0₂ = = 40 N/mm A A A 0₂ = = 40 N/mm 2 45 2 A B On 2 0₁ = 60 N/mmarrow_forward1. The stress condition on a two-dimensional infinitesimal material element is shown in Fig. 1 Fig. 1 60 MPа A 50 MPа В 30 MPа A. Describe the state of stress on: (i) Face A (ii) Face B B. State the sign convention for stress components on faces A and B in the: (i) Physical-space (ii) Mohr-Circle-space C. Draw the Mohr circle for the stress element in Fig. 1arrow_forwardQ/1/The state of plane stress at a point is shown on the element . Represent this state of stress on an element oriented 15 counterclockwise from the position shown. 30 MPd b’OMIoD‘ go M¥Paarrow_forward
Recommended textbooks for you

 Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON
Structural Analysis (10th Edition)Civil EngineeringISBN:9780134610672Author:Russell C. HibbelerPublisher:PEARSON Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning
Principles of Foundation Engineering (MindTap Cou...Civil EngineeringISBN:9781337705028Author:Braja M. Das, Nagaratnam SivakuganPublisher:Cengage Learning Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
Fundamentals of Structural AnalysisCivil EngineeringISBN:9780073398006Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel LanningPublisher:McGraw-Hill Education
 Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning
Traffic and Highway EngineeringCivil EngineeringISBN:9781305156241Author:Garber, Nicholas J.Publisher:Cengage Learning


Structural Analysis (10th Edition)
Civil Engineering
ISBN:9780134610672
Author:Russell C. Hibbeler
Publisher:PEARSON

Principles of Foundation Engineering (MindTap Cou...
Civil Engineering
ISBN:9781337705028
Author:Braja M. Das, Nagaratnam Sivakugan
Publisher:Cengage Learning

Fundamentals of Structural Analysis
Civil Engineering
ISBN:9780073398006
Author:Kenneth M. Leet Emeritus, Chia-Ming Uang, Joel Lanning
Publisher:McGraw-Hill Education


Traffic and Highway Engineering
Civil Engineering
ISBN:9781305156241
Author:Garber, Nicholas J.
Publisher:Cengage Learning