
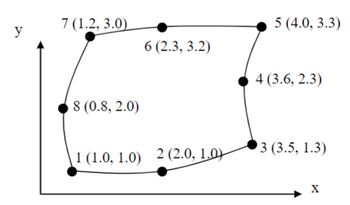
Calculate the stiffness matrix for the Q8 element shown below. Make use of the shape functions in natural coordinates and the Jacobian calculated in previous problems. Use 2x2 Gaussian numerical integration. Use plane strain conditions (for unit thickness) with E=200E9 (MPa) and nu=0.25.
I have attached my matlab code below. Please look thru it and correct it. Thanks.
u=sym('u') %%zta
v=sym('v') %%eta
x1=1
x2=2
x3=3.5
x4=3.6
x5=4.0
x6=2.3
x7=1.2
x8=0.8
y1=1
y2=1
y3=1.3
y4=2.3
y5=3.3
y6=3.2
y7=3.0
y8=2.0
X=[x1;x2;x3;x4;x5;x6;x7;x8]
Y=[y1;y2;y3;y4;y5;y6;y7;y8]
%% diff of zta
DN1Du=1/4*(1-v)*(2*u+v);
DN2Du=-u*(1-v);
DN3Du=1/4*(1-v)*(2*u-v);
DN4Du=1/2*(1-v^2);
DN5Du=1/4*(1+v)*(2*u+v);
DN6Du=-u*(1+v);
DN7Du=1/4*(1+v)*(2*u-v);
DN8Du=-1/2*(1-v^2);
%% diff of eta
DN1Dv=1/4*(1-u)*(2*v+u);
DN2Dv=-1/2*(1-u^2);
DN3Dv=1/4*(1+u)*(2*v-u);
DN4Dv=-v*(1+u);
DN5Dv=1/4*(1+u)*(2*v+u);
DN6Dv=1/2*(1-u^2);
DN7Dv=1/4*(1-u)*(2*v+u);
DN8Dv=-v*(1-u);
%% find dx/du dx/dv, dy/du and dy/dv
a=[DN1Du, DN2Du, DN3Du, DN4Du, DN5Du, DN6Du,DN7Du, DN8Du]
dxdu=a*X
b=[DN1Dv, DN2Dv, DN3Dv, DN4Dv, DN5Dv, DN6Dv, DN7Dv,DN8Dv]
dxdv=b*X
dydu=a*Y
dydv=b*Y
%% Jacobian
J=dxdu*dydv-dxdv*dydu
%% define DNiDx
DN1Dx=1/J*(dydv*DN1Du-dydu*DN1Dv)
DN2Dx=1/J*(dydv*DN2Du-dydu*DN2Dv)
DN3Dx=1/J*(dydv*DN3Du-dydu*DN3Dv)
DN4Dx=1/J*(dydv*DN4Du-dydu*DN4Dv)
DN5Dx=1/J*(dydv*DN5Du-dydu*DN5Dv)
DN6Dx=1/J*(dydv*DN6Du-dydu*DN6Dv)
DN7Dx=1/J*(dydv*DN7Du-dydu*DN7Dv)
DN8Dx=1/J*(dydv*DN8Du-dydu*DN8Dv)
%% defrine DniDx
DN1Dy=1/J*(-dxdv*DN1Du+dxdu*DN1Dv)
DN2Dy=1/J*(-dxdv*DN2Du+dxdu*DN2Dv)
DN3Dy=1/J*(-dxdv*DN3Du+dxdu*DN3Dv)
DN4Dy=1/J*(-dxdv*DN4Du+dxdu*DN4Dv)
DN5Dy=1/J*(-dxdv*DN5Du+dxdu*DN5Dv)
DN6Dy=1/J*(-dxdv*DN6Du+dxdu*DN6Dv)
DN7Dy=1/J*(-dxdv*DN7Du+dxdu*DN7Dv)
DN8Dy=1/J*(-dxdv*DN8Du+dxdu*DN8Dv)
%% B matrix
B=[DN1Dx, 0, DN2Dx, 0, DN3Dx, 0, DN4Dx, 0, DN5Dx, 0, DN6Dx, 0, DN7Dx, 0, DN8Dx, 0;
0, DN1Dy, 0, DN2Dy, 0, DN3Dy, 0, DN4Dy, 0, DN5Dy, 0, DN6Dy, 0, DN7Dy, 0, DN8Dy;
DN1Dy, DN1Dx, DN2Dy, DN2Dx, DN3Dy, DN3Dx,DN4Dy,DN4Dx,DN5Dy,DN5Dx,DN6Dy,DN6Dx, DN7Dy,DN7Dx,DN8Dy,DN8Dx;]
BT=transpose(B)
%% define D strain E=200*10^9 nu=0.25
Q=200*10^9/((1+0.25)*(1-2*0.25))
R=[1-0.25, 0.25, 0;
0.25, 1-0.25, 0;
0, 0, (1-2*0.25)/2;]
D=Q*R
%%
u1=-1/sqrt(3);
v1=-1/sqrt(3);
u2=1/sqrt(3);
v2=1/sqrt(3);
w1=1;
w2=1;
% Substitute u and v with u1 and v1
J_sub = subs(J, [u, v], [u1, v1]);
B_sub = subs(B, [u, v], [u1, v1]);
BT_sub = subs(BT, [u, v], [u1, v1]);
F1=BT_sub*D*B_sub*J_sub
% Substitute u and v with u1 and v2
J_sub2 = subs(J, [u, v], [u1, v2]);
B_sub2 = subs(B, [u, v], [u1, v2]);
BT_sub2 = subs(BT, [u, v], [u1, v2]);
F2=BT_sub2*D*B_sub2*J_sub2
% Substitute u and v with u2 and v1
J_sub3 = subs(J, [u, v], [u2, v1]);
B_sub3 = subs(B, [u, v], [u2, v1]);
BT_sub3 = subs(BT, [u, v], [u2, v1]);
F3=BT_sub3*D*B_sub3*J_sub3
% Substitute u and v with u2 and v2
J_sub4 = subs(J, [u, v], [u2, v2]);
B_sub4 = subs(B, [u, v], [u2, v2]);
BT_sub4 = subs(BT, [u, v], [u2, v2]);
F4=BT_sub4*D*B_sub4*J_sub4
F=(F1*w1*w2)+(F2*w1*w2)+(F3*w1*w2)+(F4*w1*w2);
Trending nowThis is a popular solution!
Step by stepSolved in 3 steps with 2 images

- 4arrow_forwardHW 2_2 The volume of a partially-filled spherical tank can be computed as: V = πα 3 (3R – d); where d is the depth of the water in the tank (m) and R is the radius of the tank (m). Given that R=3m, to what depth must the tank be filled so that it holds 30 m³? Write a PYTHON code & implement the bisection algorithm to answer the question correct to 3 sig figs. Plot to select your own initial guesses. Display the answer in an informative sentence, using formatted printing.arrow_forwardThe same element (as per previous question) is considered here again. Suppose that [J11 J12] the Jacobian matrix can be written in the form of J = J21 J22 value of J21 for a point located at (§, n)-(-0.05,-0.50). (Hint: round you final answer to 4 digits after decimal point). y 4 (1,6) 1 (0, 0) 2 (3, 2) 3 (5,5) Find the Xarrow_forward
- 6arrow_forwardTopics Discussed: Static of Rigid Bodies, Force Vector, Addition of a System of Coplanar Forces, Cartesian Vector Please re-compute and re-solve the given, This is my answer. But I also want to see your expert answer if we land in the same solutions and answers. Please show your complete solution. Thank you.arrow_forwardSecond m oment of area of a section: With respect to the x axis: I [[ v²dxdy D 8. A plate is bounded by the positive x and y axes and the curve y=3-\x . Find the second moment of area of the plate with respect to the x-axis. [ANS : 8.1]arrow_forward
- The dependence of the tensions t (units: N) in a structure on the external forces f (units: N) follows the linear system Ct=f, where both t and f are 5 by 1 column vectors. The coefficient matrix C has been determined to be [ 11 14 20 -5 -19 ] -5 7 -3 5 -6 4 -5 13 -2 -10 0 0 0 12 -10 0 0 0 0 14 By how many N would the external force f2 need to be decreased (while all other external forces stay the same) in order to decrease the tension t3 by 94 N?arrow_forwardEdition Eighth Z▼▲ Ā Mc Graw Hill Vector Mechanics for Engineers: Statics HW: Ch 6 จงหาตำแหน่งของจุดศูนย์ถ่วงของชิ้นส่วนเครื่องจักรกลด้านแกน x ของวัสดุประกอบดังรูป Find the position of the center of gravity of the mechanical part on the x-axis side of the composite as shown in the figure. mm 20 34 mm 62 mm 51 mm 20 mm 200 mm 10 mm © 2007 The McGraw-Hill Companies, Inc. All rights reserved. 45 m 100 mm 55 mm 7-52arrow_forwardQ6arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





