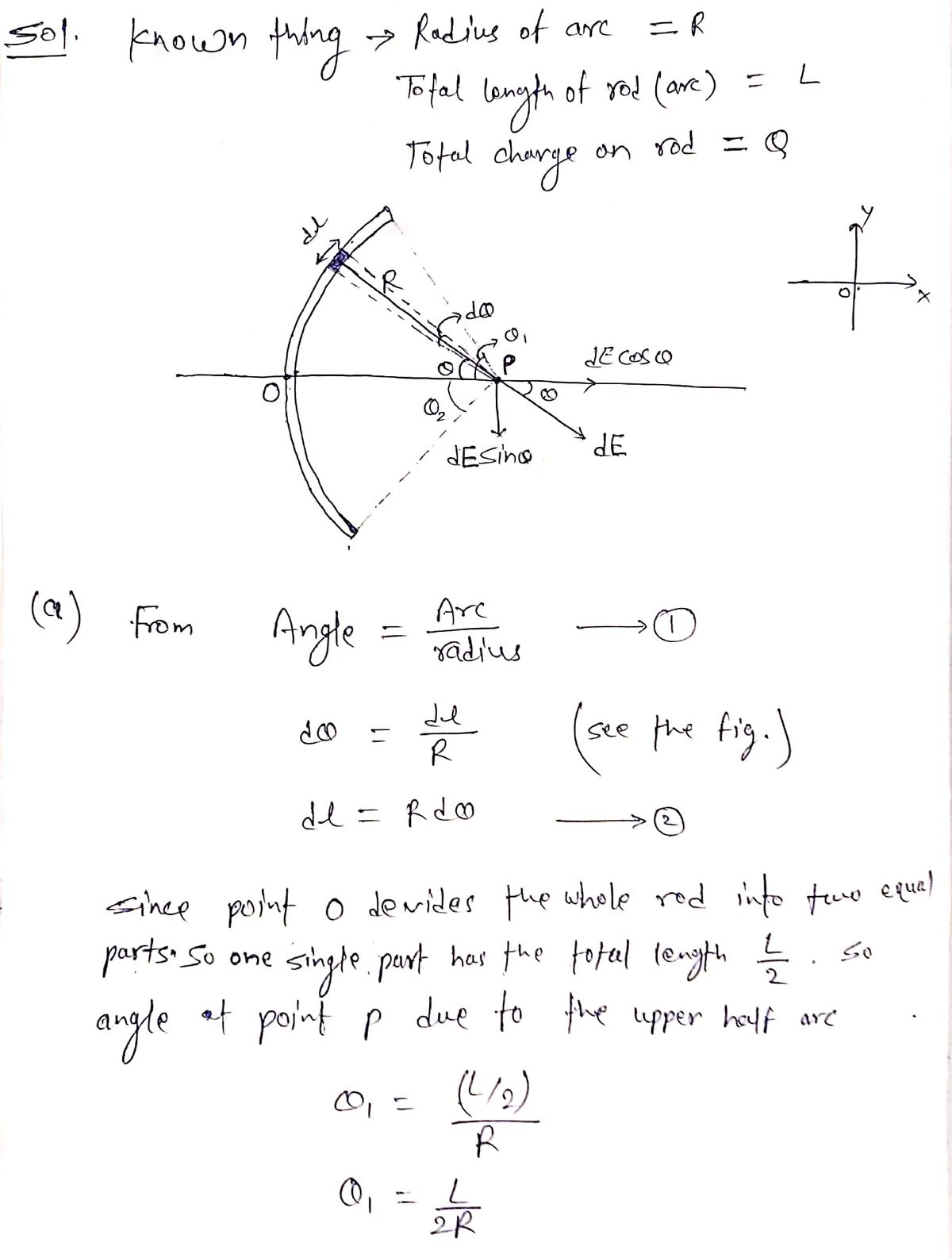
A uniformly charged rod of length L is bent into an arc of radius R. Total charge on the rod is Q. This is the arc problem we considered in class. ( R P (a) Find the angle in radians, 0, subtended by the arc and the linear charge density λ in terms of Q, L and R. See the exercises and the hints and guide at the end of the homework for a reminder of the relationship between angle and arc length. (b) Find the field at a test point placed at the center of the circle that the arc is part of. Again, follow the process, and remember that the sample charge dq occupies a small length of the rod, and that length is now a small part of an arc. (c) Check that your results for the case L << R give you the field of a point source with charge Q, a distance R away. You will want to use the small angle approximation from the exercises: sin for 0 << 1
A uniformly charged rod of length L is bent into an arc of radius R. Total charge on the rod is Q. This is the arc problem we considered in class. ( R P (a) Find the angle in radians, 0, subtended by the arc and the linear charge density λ in terms of Q, L and R. See the exercises and the hints and guide at the end of the homework for a reminder of the relationship between angle and arc length. (b) Find the field at a test point placed at the center of the circle that the arc is part of. Again, follow the process, and remember that the sample charge dq occupies a small length of the rod, and that length is now a small part of an arc. (c) Check that your results for the case L << R give you the field of a point source with charge Q, a distance R away. You will want to use the small angle approximation from the exercises: sin for 0 << 1
Related questions
Question

Transcribed Image Text:A uniformly charged rod of length L is bent into an arc of radius R. Total charge on the rod is Q.
This is the arc problem we considered in class.
(
R
P
(a) Find the angle in radians, 0, subtended by the arc and the linear charge density λ in terms of Q,
L and R. See the exercises and the hints and guide at the end of the homework for a reminder
of the relationship between angle and arc length.
(b) Find the field at a test point placed at the center of the circle that the arc is part of. Again,
follow the process, and remember that the sample charge dq occupies a small length of the rod,
and that length is now a small part of an arc.
(c) Check that your results for the case L << R give you the field of a point source with charge
Q, a distance R. away. You will want to use the small angle approximation from the exercises:
sin for 0 << 1
(d) With minimal reanalysis (just note where you need to change the work you did above and how
that changes the result) find the field at the test point if we replace the charge on half the rod
with the opposite charge, so we have +Q/2 on a length L/2 and -Q/2 on the remaining length
L/2.
R
* P
(e) Show that the results with this new distribution, in the L << R limit is consistent with a dipole
that has dipole moment p=(Q/2)(L/2) = QL/4 and is oriented tangent to the arc (perpendicular
to R). You will want to use the correct small angle approximation for cosine (see the exercises!)
Expert Solution
Step 1
Trending now
This is a popular solution!
Step by step
Solved in 5 steps with 4 images

Follow-up Questions
Read through expert solutions to related follow-up questions below.